Exercice 1 – Algèbre de Boole
a) En utilisant exclusivement l’algèbre booléenne, démontrez que :
b) En utilisant la décomposition de Shannon, démontrez que :
c) En utilisant une technique de votre choix, démontrez que le circuit suivant a toujours sa sortie fausse :
1) La fonction FX est spécifiée par sa table de vérité :
Trouver l’expression disjonctive simplifiée de X au moyen de la table de Karnaugh.
Évaluez son coût minimal et dessinez votre meilleur circuit
2) La fonction FY a déjà été réalisée par un apprenti. Elle fonctionne bien mais le patron prétend que le circuit coûte trop cher pour rien. Faites l’analyse de cette fonction et proposez votre meilleur circuit en comparant les versions disjonctive et conjonctive.
1) Retranscrire les minterms de la fonction F sous forme binaire en soulignant les minterms facultatifs — exemple : 0110 pour

2) Procéder par la méthode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliquants premiers
3) Utiliser la table suivante pour identifier les impliquants essentiels de F(A,B,C,D)
b) En utilisant la décomposition de Shannon, démontrez que :
c) En utilisant une technique de votre choix, démontrez que le circuit suivant a toujours sa sortie fausse :
Exercice 2 – Analyse et synthèse de circuits
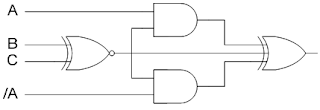
L’implantation d’une fonction logique Z relativement complexe repose sur
un NOR de deux autres fonctions FX et FY comme indiqué sur le schéma
suivant :
1) La fonction FX est spécifiée par sa table de vérité :
Trouver l’expression disjonctive simplifiée de X au moyen de la table de Karnaugh.
Évaluez son coût minimal et dessinez votre meilleur circuit
2) La fonction FY a déjà été réalisée par un apprenti. Elle fonctionne bien mais le patron prétend que le circuit coûte trop cher pour rien. Faites l’analyse de cette fonction et proposez votre meilleur circuit en comparant les versions disjonctive et conjonctive.
c) Votre patron vous demande de porter un regard critique sur la première implantation de FY. Qu’allez-vous lui dire ?
3) Sachant que finalement, seule la valeur de Z importe, proposez votre meilleur circuit pour implanter Z(A,B,C,D)
Exercice 3 - Quine-McCluskey
Soit la table de vérité de la fonction logique F(A,B,C,D) :
1) Retranscrire les minterms de la fonction F sous forme binaire en soulignant les minterms facultatifs — exemple : 0110 pour

2) Procéder par la méthode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliquants premiers
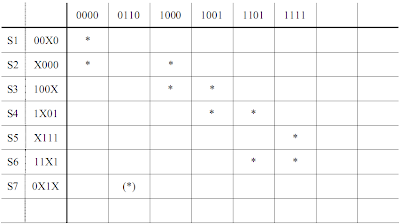
3) Utiliser la table suivante pour identifier les impliquants essentiels de F(A,B,C,D)
4) Utilisez la méthode de Petrick simplifiée (après élimination
des impliquants essentiels) pour trouver toutes les solutions (les moins
chères) possibles. Écrivez chaque solution sous sa forme algébrique
(disjonctive).
5) Confirmez votre résultat en utilisant une table de Karnaugh
Exercice 4 - Décodeur
En utilisant un décodeur (3 bits de sélection A, B et C) et une seule
porte logique à deux entrées par fonction, implantez les fonctions F1,
F2, F3 et F4
Exercice 5 - multiplexeur
En utilisant un multiplexeur (4 vers 1, 2 bits de sélection) et une seule porte logique, implantez la fonction suivante :






ConversionConversion EmoticonEmoticon
Remarque : Seul un membre de ce blog est autorisé à enregistrer un commentaire.